Das Schulprojekt „Römerschiff“ im Gymnasium an der Stadtmauer Bad Kreuznach. Ein archäologisches Experiment
Der Victorinus-Code®, Teil 3
von Walther Krumme
in Zusammenarbeit mit: Theodor Bartel, Raphael Erdmann, Keanu Firros, Markus Gräff, Jan Marek Krummenau, Niklas Schopperth, Julian Selonke.
0.1.1. Einleitung
In der bereits vorgelegten Untersuchung „Ein römisches Segelboot mit Dschunken-Segel im Oceanus-Mosaik Bad Kreuznach. Der Victorinus-Code, Teil 2“ ging es um den Nachweis des historischen Konstruktionsansatzes. Das Musterblatt des Mosaizisten wurde durch Analyse der einzelnen Zirkelschläge rekonstruiert. Dabei wurde der wissenschaftliche Nachweis der Übereinstimmung von rekonstruiertem Musterblatt und tatsächlichem Mosaik bewusst ausgespart. Dazu hatten junge Menschen der gymnasialen Mittel- und Oberstufe die Möglichkeit, in direkter Teilhabe an der Forschungsarbeit an einem antiken Meisterwerk ihrer Stadt mitzuarbeiten: die Zeichnung des mit dem „Victorinus-Code“ erschlossenen Musterblattes eines römischen Segelbootes im angenommenen Maßstab 1:1 eines „richtigen“ Römerschiffes auf den Schulhof wie auf den Boden einer „römischen Werft“ und dem Vergleich dieser Zeichnung mit dem Original im Mosaik durch eine Luftaufnahme, die durch Ingenieur und Graphiker D. Kirschner M. Sc. digital über das Original gelegt wird. Damit kann wie unter einem Mikroskop die Übereinstimmung der Linienführungen genau geprüft werden. In Zusammenarbeit mit Daniel Kirschner wird der Exkurs vorgelegt: Der zergliederte Mast. Eine Beobachtung zur Kompositionstechnik des Meisters Victorinus.
0.2.2. Zielsetzung und Vorüberlegungen
Als Ziele des Experimentes werden definiert:
- Es soll geprüft werden, ob das rekonstruierte Musterblatt des Segelbootes etwa in der Größe eines realen Römerschiffes mit einer geschätzten Rumpflänge von 9 m auf den Boden des Schulhofes vermutlich wie auf einer römischen Werft mit Zentrierstock, Hanfschnüren und Kreidehaltern gezeichnet werden kann.
- Durch digitale Überlagerung der Fotodatei des Originals über die Luftaufnahme des zeichnerischen Experimentes soll dessen Übereinstimmung mit dem Original geprüft werden.
0.3.3. Das Experiment
0.3.1.3.1. Hilfsmittel zur Durchführung des Experimentes
- Die geeignete Fläche von etwa 10m x 10m wurde im Innenschulhof des Stadtmauergymnasiums Bad Kreuznach gefunden.
- Die Messschnüre wurden aus ca. 2mm starken Hanfschnüren geschnitten. Der Einsatz von Messschnüren im römischen Konstruktionsvorgang eines Schiffes wird aus der Verlege-Technik des Mosaiks selbst abgeleitet: Die Segelränder sind mit einer Messschnur mit dem Victorinus-Maß r = OE gelegt und dann höchstwahrscheinlich in den Estrich abgedrückt worden.
- Ein Holzstab mit zentrierter Metallspitze diente als Zirkelstandfuß.
- Eine selbst konstruierte und gebaute hölzerne Kreidehalterung ermöglichte die beidhändige, winkeltreue Führung und das Nachladen mit Straßenkreide.
- Zur besseren Sichtbarmachung wurde im Kompromiss handelsübliche Straßenkreide verwendet.
0.3.2.3.2. Die Durchführung auf dem Schulhof

- Abb. 1: Die mitarbeitenden Schüler Theodor Bartel, Raphael Erdmann, Keanu Firros, Markus Gräff, Jan Marek Krummenau, Niklas Schopperth, Julian Selonke sind hier zur Gruppenaufnahme zusammengestellt, tatsächlich arbeitete ein Messtrupp nach dem anderen. Ganz rechts Herr L. Luckhaupt vom Institut für Geschichtliche Landeskunde, Mainz, dem die Schüler das Projekt präsentierten.[Bild: B. Schulz]
- Zunächst wurde das „Werftplanum“ mit r = OA im Vollkreis umrissen.
- Nach Fertigstellung des Pentagons wurden die Messschnüre auf die Maße des Victorinus-Codes kalibriert.
- Immer zwei von acht Schülern stellten einen über den anderen Messtrupp, der nach Anweisung des Projektleiters die 83 Konstruktionsschritte konzentriert und genau durchführte.
- Ob das Ziel des Experiments, der Nachweis der Übereinstimmung von erschlossenem Musterblatt und Original, erreicht wurde, kann nur durch eine möglichst verzerrungsfreie Luftaufnahme wissenschaftlich beurteilt werden. Lukas Kistner (Klasse 12) pilotierte seine Drohne in 25m Höhe über die Zeichnung und legte exakt über dem Konstruktionspunkt O eine Fotostrecke an.
0.3.3.3.3. Das Ergebnis
3.3.1. Die Prüfung von Mast und Segel
Ersichtlich sind die perfekte Übereinstimmung des Mastes und die sehr hohe Übereinstimmung des Segels mit dem Original. Durch die sorgfältige Arbeit der Schüler, die die aus dem Mosaik erschlossene Arbeitsweise des Mosaizisten selbstständig imitierten, kann als bewiesen gelten: die Segelränder sind mit einer Messschnur im Victorinus-Maß OE gelegt worden.
Deutlich wird auch, dass unter technischen Gesichtspunkten so kein Aufriss für Mast und Segel auf einer römischen Werft ausgesehen haben kann. Der Mast wird vom römischen architectus mit Sicherheit in einer Flucht gezeichnet worden sein. Damit die Abweichung des Topmastes im Mosaik umso deutlicher sichtbar wird, ist der Mastbaum bewusst auf die Pflaster- Markierungen des Schulhofes gezeichnet worden.
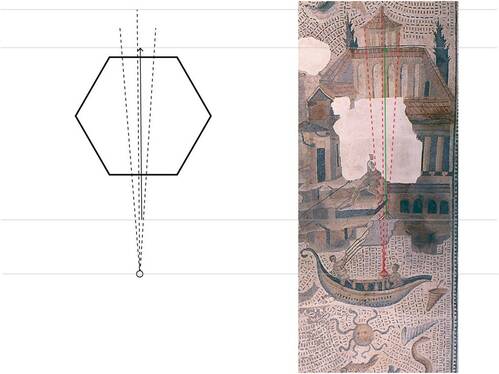
3.3.2. Exkurs: Der zergliederte Mast. Eine Beobachtung zur Kompositionstechnik des Meisters Victorinus. In Zusammenarbeit mit Daniel Kirschner
Bereits bei der Analyse der Künstlersignatur des Meisters Victorinus [Anm. 1] wurde das Stilmittel des „provozierenden Schiefstandes“ festgestellt, mit dem der Künstler auf weit ausgreifende Konstruktionslinien im Mosaik aufmerksam macht. In der Bildinsel „Kunsthafen“ provoziert jetzt der Künstler mit dem ästhetischen und technischen Ärgernis der Darstellung eines zergliederten Mastes, die nach der Logik seiner Kompositionstechnik auf weit ausgreifende, die Bergungsschnitte einzelner Mosaikschollen übergreifende Kompositionslinien aufmerksam macht. Diese mit bloßem Auge nicht feststellbare Linienführung wurde von Daniel Kirschner digital sichtbar gemacht:
Der Mastbaum von der Basis bis Punkt 12 des Konstruktionsplanes [Anm. 2] zeigt in salvatorischer Funktion (der Matrose klammert sich an den rettenden Mastbaum) auf den Pinienzapfen des pyramidalen Tempeldaches (mittlere, gestrichelte Linie). Davon graduell differenziert, zielt der Toppmast in navigatorischer Funktion (durchgezogener Peilstrahl) auf einen im Mosaik genau markierten Schnittpunkt einer Säulenbasis des Tempeldaches mit dem Dachfirst eines kolossalen Gebäudes. Der Sturz der Säulen, die das Tempeldach tragen, folgt Konstruktionslinien, die auf einen Messpunkt in der Hand des Matrosen fluchten.
Erneut zeigt sich, wie schon in der Analyse der Künstlersignatur nachgewiesen, dass ein einziger Mosaikstein der Messpunkt für ein ganzes Bildprogramm sein kann: Dieser wird von der linken Hand des Matrosen zusammen mit dem Mast fest umklammert und ist der Fluchtpunkt von Konstruktionslinien, der der zunächst nicht erklärbare Schiefstand der Säulen, die das pyramidale Tempeldach tragen, folgt. Dieser provozierende „o-beinige“ Schiefstand von Tempelsäulen ist für das an griechischer Klassik geschulte Auge ein Affront. Streben doch die Säulengalerien des Parthenon über den Dächern Athens in der geometrischen Figur des Pyramidenstumpfes in vollendeter Harmonie himmelwärts. (Diesen Hinweis verdankt der Verfasser Kathrin Kirschner). Der Meister Victorinus dagegen stellt das alles auf den Kopf und mutet dem Betrachter den Anblick einer Tempelarchitektur zu, die nicht nach Vorgaben klassisch griechischer Stilistik, sondern über das existentielle Erleben der oratio de profundis, dem Gebet aus der Tiefe, eingemessen wurden. Das wird ergänzt durch die Beobachtung eines Wellensymbols, das genau auf den Mund des Matrosen zeigt. Die sich in Reihe anschließenden dunklen Steine formieren sich wie ein nach oben geschwungenes Spruchband gotischer Malerei und fädeln sich ein in eine Konstruktionslinie, die auf das Tempeldach zielt. Vermutlich wird hier, in einer zweiten Deutungsebene, die clamatio, das Schreien aus tiefer Seenot, verbildlicht.
Die digitale Sichtbarmachung der Kompositionslinien macht zudem deutlich: hier ist die stein- und winkelgenaue Aneinander-Fügung der Mosaikschollen bei Wiedereinbettung geglückt.
Mit Sicherheit ist anzunehmen, dass ein in einem Windwirbel verdrehtes und umgeschlagenes Segel kein Gegenstand einer technischen Zeichnung auf einer römischen Werft gewesen sein kann. Dennoch ist der Verfasser der Meinung, dass diese kunstvoll gezirkelte Szene mit „Informationen“ aus einem real existiert habenden Riss für das Segel „konstruiert“ worden ist. (Einen Rekonstruktionsversuch des Dschunkensegels legte der Verfasser bereits vor[Anm. 3]). Es sei noch darauf hingewiesen, dass die Segelfläche des hier gezirkelten Segels 5,9 m² bei einer Rumpflänge von 9 m betragen würde. (Berechnung weiter unten).
3.3.3. Die Prüfung des Rumpfes
Wie unter einem Mikroskop kann die Übereinstimmung der Bordwand backbord vom Mast bis zum hoch aufragenden Heck mit dem Original geprüft werden. Das gilt auch für die Bordwand steuerbord ab Matrosen bis zum Heck.
Die Hilfslinie 52 zur Positionierung der Rumpfbemalung stimmt perfekt mit dem Original überein.
Der Konstruktionspunkt des Kieles ist durch den Verfasser (nicht durch die Schüler!) zu tief, der des Buges zu hoch eingemessen worden. Richtig werden sie wie folgt gezirkelt:
- Konstruktionspunkt Kiel: Setze den Zirkel mit r = AS ein in M und schneide die Senkrechte auf M nach oben: Der Schnittpunkt bezeichnet die Fingerspitzen der linken, den Mast umklammernden Hand des Matrosen.
- Setze den Zirkel ein mit r = OE in o.g. Schnittpunkt und schneide die Senkrechte auf M nach unten.
- Der korrekte Konstruktionspunkt des Buges wird mit dem Zirkel wie folgt eingemessen:
- Setze den Zirkel mit r = CE ein in den Schnittpunkt der Senkrechten auf O mit der Unterkante des Segels und schneide den Vollkreis r = OA um O nach rechts: Ansatz der Bordwand steuerbord des Bugschnabels.
- Setze den Zirkel mit r = OA ein in den Schnittpunkt 11 (Schnittpunkt der Mastflucht mit der Unterkante des Segels) und schneide den Vollkreis r = OA um O nach rechts unten: Ansatz Bordwand backbord des Bugschnabels.
Es steht trotz Korrekturen außer Zweifel, dass das Musterblatt des Segelbootes vollständig mit Victorinus-Maßen konstruiert worden ist.
Deutlich ist aber auch, dass die Risszeichnung des Rumpfes auf dem Planum einer römischen Werft so nicht ausgesehen haben kann, ist doch das Schiff im Mosaik perspektivisch gezirkelt mit einer extremen Schlagseite nach Steuerbord abgebildet. Wie tief die Steuerbordseite schon ins Wasser taucht, zeigt der Abstand der Bordkante zum ersten Wellensymbol [= Wasserlinie] ab Bug. Durch ein entsprechendes graphisches PC-Programm müsste der Rumpf nach backbord aufgerichtet werden. Auch hier ist der Verfasser der Meinung, dass „Daten“ aus einem real existiert habenden Seitenriss dieses Schifftyps in die Zeichnung des Musterblattes mit großer Wahrscheinlichkeit eingeflossen sind.
3.3.4. Die Umgebung des Segelbootes
Das herausragende, nicht avisierte Ergebnis des Versuches ist die Sichtbarmachung der künstlerischen Kompositionsweise, die die unmittelbare Umgebung des Schiffes in die technischen Konstruktionslinien mit einbezieht: Der Vollkreis r = OA und die 2. Sehne S5 des Pentagons positionieren einen rechten Winkel eines der Hafeneinfahrt vorgelagerten Küstenabschnittes, der damit wie vermessen und künstlich angelegt wirkt. Handelt es sich hier um eine künstlich angelegte Reede in unregelmäßiger Rechteckform? Auch links vom Mast wird ein weiterer rechter Winkel dieser vermuteten Reede, positioniert durch den Vollkreis r = OA und die 5. Sehne S5, wahrgenommen. Es mutet an, als ob durch den Vollkreis r = OA auch der „Operationsradius“ des Segelbootes angegeben wird: Die vermutete Reede vor einem römischen Kunsthafen und deren unmittelbare Umgebung. Diese Zusammenhänge wurden erst durch die Vergrößerung, die die Luftaufnahme ermöglichte, entdeckt. Das überdimensionale Schneckenhaus wird in seiner Positionierung durch o.g. Kreis eingemessen. Die konstruierte „Schwanzflosse“ des Schwertfisches ist eingepasst in die heckwärts verlängerte Konstruktionslinie AOB und den o.g. Kreisbogen. Die mythische Natter im Gewande einer natrix tesselata, die aus dem Heck hervorschießt, schmiegt sich perfekt an einen Kreisbogen mit dem Radius der Heckzier r = AS. Wenn die Konstruktionslinien des Schiffes so gestaltend in seine Umgebung auf der ausgesägten Mosaikscholle ausgreifen, werden sie über den Sägeschnitt hinaus auch in der unter den Kiel angelegten Mosaikscholle gestaltend wirksam sein. Diese Entdeckung der über den Sägeschnitt ausgreifenden Konstruktionslinien ermöglicht u.a. den Nachweis verkanteter Wiedereinbettung und die Rekonstruktion der originalen Mosaikoberfläche. Ungeplant beweist damit das Experiment
a. die Angemessenheit des erkenntnistheoretischen Ansatzes dieser Forschung: opus tessalatum sui ipsius interpres: Das Mosaik erklärt sich selbst, die sachgemäße Deutung dieses einzigartigen Mosaiks erfolgt entlang seiner Konstruktionslinien,
b. die mosaizistische Perfektion des römischen Meisters Victorinus: das Mosaik ist bis ins Detail steingenau durchdacht und eingemessen, wie es in diesem Experiment durch die Vergrößerung gezeigt werden konnte. Die Prüfung der Frage, ob die Mosaikschollen bei Wiedereinbettung in die Römerhalle steingenau eingepasst wurden, ist die wissenschaftliche Voraussetzung zur angemessenen Interpretation dieses Mosaiks mit seinem ganz eigenständigen Bildprogramm,
c. die Verortung der Seenotszene auf die vermutete Reede eines römischen Kunsthafens. (Zum Kunsthafen im Mosaik vergleiche „Der Victorinus-Code Teil 2“)
0.1.1.3.4. Die Maße des Schiffes
Zu den nicht erwarteten Ergebnissen des Experimentes zählt auch die Einsicht, dass sowohl die Körpermaße als auch die Körperhaltung der Besatzung über Konstruktionslinien und –punkte gespannt worden ist. Ein Vergleich von Abb. 2 mit Abb. 3 macht deutlich: zuerst waren die Konstruktionslinien, dann die Körpermaße. Insbesondere die Fingerspitzen sind so angelegt, dass sie auf wichtige Mess- bzw. Schnittpunkte zeigen. Das wurde bereits am überlangen rechten Arm des Steuermannes des Seeruderschiffes dieses Mosaiks festgestellt, der vom Mosaizisten so lange ausgedehnt wurde, bis die Daumenspitze einen wichtigen Schnittpunkt dreier Kreisbögen anzeigt. Demnach können die Maße des Schiffes nicht über Elle, Fuß und Spanne der Besatzung rekonstruiert werden. Der Gegensatz zur Künstlersignatur dieses Mosaiks, in der das sehr eigenwillige Körpermaß „Kopf des Künstlers“ die kalligraphische Anordnung von Buchstaben und eine Küstenlinie formatierte, ist offenkundig.[Anm. 4]
Sollte das Segelboot tatsächlich auf der Reede eines römischen Kunsthafens im Einsatz gewesen sein, hätte der Rumpf bestimmten konstruktiven Anforderungen genügen müssen. Zum Abreiten der Dünung empfiehlt sich ein gebogener Kiel. Zur Fahrt ganz in Küstennähe unter Segel wird eine ungefähre Rumpflänge von etwa 9m, nicht weniger, von Vorteil sein. Wird dann das römische Fuß mit 30 cm angenommen, können alle Maße des Victorinus-Codes und damit die Größe des Schiffes im heutigen Längenmaß berechnet werden: Wenn AOB = 9m = 30 römische Fuß, dann r = OA = 4,50m = 15 römische Fuß usw. Die Segelfläche umfasst bei dieser angenommenen Rumpflänge von 30 Fuß: 5,9 m² (Segelrand = OE = Faktor 1,3 = 2,77m; Unterliek = Faktor 1 = 2,13m).
Wenn OA = 4,50m dann ist AS = 68 cm. AS entspricht der Höhe der Amphoren im Segelboot.
0.1.2.3.5. Fazit
- Die Kompositionstechnik mit aneinandergefügten Kreisbögen, deren Radien sich aus dem Victorinus-Code berechnen, kann als bewiesen gelten.
- Die Entdeckung der z.T. weit über den Sägerand der Mosaikschollen hinausreichenden Konstruktionslinien ermöglicht die Überprüfung und ggfls. Korrektur ihrer Position auch nach verkanteter Wiedereinbettung.
- Die Körpermaße der Besatzung sind über die Konstruktionslinien gespannt und fallen damit für die Berechnung von Schiffsmaßen aus.
- Das Experiment hat gezeigt, dass es tatsächlich möglich ist, das rekonstruierte Musterblatt wie einen Seitenriss in der angenommenen Größe eines realen Römerschiffes mit den Hilfsmitteln Messschnüre, Zentrierstock und Kreide auf ein Planum zu zeichnen.
0.2.Nachweise
Verfasser: Walther Krumme
Red. Bearb.: Lutz Luckhaupt
Anmerkung:
Victorinus-Code ist als Marke unter der Nummer 30 2019 223 002 beim Deutschen Patent- und Markenamt eingetragen.
Verwendete Literatur:
Der Aufsatz baut auf den Ergebnissen der beiden Aufsätze Victorinus-Code Teil 1 und 2 von Walther Krumme auf.
Erstellt am: 08.10.2019