Ein römisches Segelboot mit Dschunken-Segel im Oceanus-Mosaik Bad Kreuznach. Nachweis des historischen Konstruktionsansatzes. Zum 25. Jubiläum des Museums für antike Schifffahrt in Mainz
Der Victorinus Code ®, Teil 2.
von Walther Krumme
Erst das komplexe Zusammenspiel von verschiedensten Forschungsdisziplinen, der Naturwissenschaft, Restaurierung und Geschichte führt zu neuen Erkenntnissen.
(Wandschrift im Museum der Pfalz, Speyer)
0.1.1. Einleitung
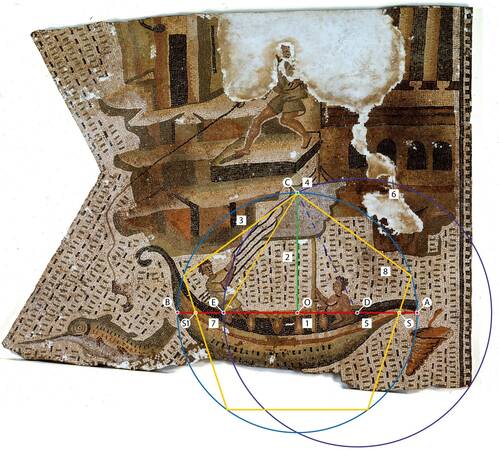
Es wird von der Annahme ausgegangen, dass das Segelboot nicht freihändig, sondern über ein sorgfältig konstruiertes Musterblatt vom römischen Mosaizisten Victorinus in die dritte Konstruktionsebene [Anm. 1] des Oceanus-Mosaik in der Römerhalle Bad Kreuznach eingemessen worden ist. Dieses Mosaik bildet insgesamt fünf Schiffe ab: Ein hochseetaugliches Seeruderschiff, ein Beiboot im Schlepp, ein Frachtschiff unter Segel für den Binnen- und Küstennahverkehr sowie zwei kleine geruderte Fischernachen. Das Mosaik ist mit einer durchkonstruierten Künstlersignatur versehen, die Namen und Seitenporträt des Künstlers Victorinus wiedergibt.[Anm. 2]
Die vorgelegte Untersuchung wird zeigen, dass das vollständig erhaltene Segelboot (Abb. 2) nicht freihändig verlegt, sondern in mehr als 80 Schritten ganz sorgfältig mit dem Victorinus-Code konstruiert wurde. Dieses Gestaltungsprinzip wurde vom Verfasser bei der Analyse der Künstlersignatur des römischen Mosaizisten Victorinus entdeckt und dechiffriert und besagt, dass die jeweils verwendeten Konstruktionsmaße aus einem zirkelkonstruierten Pentagon nach Ptolemäus generiert werden.[Anm. 3] Die aus dem Pentagon des Segelbootes generierten zwölf Maße sind auf der rechten Seite des auf Papyrus rekonstruierten Musterblattes (Abb. 4) aufgelistet. Die Entdeckung dieser Konstruktionszeichnungen wird weiter unten in der Form geometrischer Textaufgaben allgemein überprüfbar protokolliert. Der Schwerpunkt der Analyse des Schiffrumpfes wird in dem Nachweis liegen, dass der erhaltene Bug mit einer Auswahl aus den zwölf aus dem Pentagon generierten Maßen zirkelkonstruiert ist. Das Heck wird nur in seinen Umrisslinien dargestellt. Entdeckt wurde auch, dass das Mosaik exakte Angaben zur Rekonstruktion des Dschunken-Segels im Hochrechteck überliefert, dessen Verhältnis von Breite zur Höhe sich wie 1:1,3 verhält (Abb. 5). Wenn der naturwissenschaftlich begründete Nachweis gelingt, dass auch das Segelboot nach dem gleichen Konstruktionsprinzip wie die Künstlersignatur mosaizistisch gestaltet ist, kann von einer systemimmanenten Beweisführung zum Nachweis des Victorinus-Codes im Oceanus-Mosaik Bad Kreuznach gesprochen werden.
0.2.2. Protokoll der Konstruktionsanalyse
0.2.1.2.1. Die Entdeckung des Pentagons nach Ptolemäus in der Abbildung des Segelbootes
Es wird angenommen, dass die bei der Analyse der Künstlersignatur beobachteten Gestaltungsprinzipien (Maße, die aus dem Pentagon generiert werden; Raster parallel verschobener Linien usw.) auch in der Konstruktionszeichnung des Segelbootes zur Anwendung kamen.[Anm. 4]
Um die Prüfung der vorgelegten Thesen zu ermöglichen, ist das Protokoll der Entdeckung der nachfolgenden Konstruktionsanalyse in Form von Textaufgaben zur Geometrie verfasst.
Das Mosaik erschließt sich selbst aus der Zusammenschau „mikroskopischer“, steingenauer Feinheiten (vgl. Nr. 56) und makroskopisch ausgreifender Linienführung, die sogar die Himmelsrichtungen miteinschließt.
- Es wird in Abb. 2 und 3 beobachtet und erwogen: Die herausgehobene, mit vier statt drei schwarzen Mosaiksteinchen gearbeitete Öffnung der dritten Amphore (ab Heck gezählt), könnte dem Augenschein nach der Mittelpunkt O einer für das Pentagon konstitutiven Strecke AOB sein. (Die Rekonstruktion des Seeruderschiffes wird zeigen, dass dort der Punkt O ebenfalls mosaizistisch besonders hervorgehoben ist).
- Über diesen angenommenen Punkt O hat der Meister Victorinus sieben Wellen (= mit drei oder vier dunklen Mosaiksteinen gebildete kleine Striche) genau auf Linie positioniert. Versuchsweise wird diese siebenfach gestrichelte Linie als Senkrechte über O aufgefasst.
Im rechten Winkel zu dieser Senkrechten wird eine Strecke AOB analog zur Künstlersignatur angelegt. Punkt A dieser Strecke AOB markiert dann die äußerste Spitze des Bugschnabels steuerbord. Wird dann A über O gespiegelt, wird die Position von B gewonnen. - Setze jetzt den Zirkel mit r = OA ein in O und schlage einen Vollkreis.
- Der Schnittpunkt mit der Senkrechten über O = C.
- Halbiere OA = D
- Setze den Zirkel mit r = DC ein in D.
- Ziehe jetzt den Kreisbogen von C auf AOB = E.
- Setze den Zirkel mit r = CE (= S5 des Pentagons nach Ptolemäus) ein in C und konstruiere des Pentagon rechts herum. Der Schnittpunkt der 2. Sehne S5 mit AD = S, der Schnittpunkt der vierten Sehne S5 mit BE = S1.
Behauptet wird: Aus den Unterteilungen von AOB lassen sich alle technischen Umrisslinien des Segelbootes konstruieren, indem diese Maße als Radien oder Längenmaße bei der Konstruktion eingesetzt werden (= Victorinus-Code).
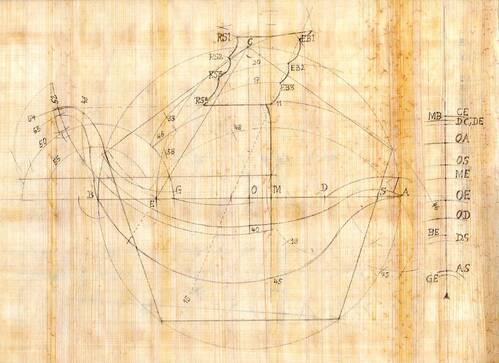
- Abb. 4: Rekonstruktionsversuch des römischen Musterblattes für das Segelboot mit Graphit auf Papyrus. Dabei wird angenommen, dass die römischen Zirkelschmiede Zirkel mit Einsätzen herstellen konnten. Der archäologische Beweis für diese Annahme steht jedoch noch aus. Die im Kompromiss zum Textbezug verwendeten arabischen Ziffern beziehen sich auf die Nummern der nachfolgenden Konstruktionsanalyse. Auf der rechten Seite sind die zwölf (DC = DE) aus dem Pentagon generierten Maße angegeben. [Bild: Walther Krumme]
0.2.2.2.2. Die Konstruktion von Mast und Segel
Das im Mosaik abgebildete Seeruderschiff hat einen kurzen, stämmigen Mast mit aufgehängtem Rahsegel für stürmische Hochseefahrten, das Segelboot dagegen hängt ein aufgelattetes Rechtecksegel am schlanken Mast hoch über die Lee der Uferbewachsung von Binnengewässern. Beiden Schiffen gemeinsam ist: der Mast wird gegen die Fahrtrichtung aus der Flucht gebogen, die Rahe ist in Fahrtrichtung nach oben verzogen.
9. Setze den Zirkel mit r = AS ein in O und schneide AOB bugwärts = M, Ansatz des Mastes auf AOB. Errichte über diesen Schnittpunkt eine Senkrechte bis zur Spiegelachse W - O des Brunnenhexagons = Mastseite bugwärts.
10. Setze den Zirkel mit r = DC ein in B und schneide AOB = Ansatz Mast vom Heck aus gesehen. Errichte über diesen Schnittpunkt eine Senkrechte wie 9. Die Strecke zwischen den Schnittpunkten 9 und 10 auf AOB bezeichnet den Mastdurchmesser.
11. Setze den Zirkel mit r = OE ein in M und schneide die Senkrechte über M = Ansatz der Unterkante des Segels.
12. In diesen Schnittpunkt 11 setze den Zirkel mit r = GE (G = BO:2) und schneide die Senkrechte über M nach unten. Ab diesem Schnittpunkt biegt sich der Mast heckwärts.
13. Der Topmast signalisiert wieder das bereits in der Künstlersignatur beobachtete „Stilmittel des demonstrativ provozierenden Schiefstandes“ [Anm. 5] und folgt der Linienführung der Senkrechten über M, jedoch um zwei Steine bugwärts versetzt, sodass er genau parallel zur Wand mit massiven Tonnengewölben, gedeutet als Mole, gesetzt ist und die Sicht auf eine sehr enge, künstlich (über das Lineal gezogene Linien) angelegte Hafeneinfahrt freigibt. Diese Position des Topmastes beschreibt wohl die „Normalflucht“ des Mastes im Gegensatz zur dargestellten gefährlichen Verbiegung nach steuerbord achtern direkt unterhalb des Segels (vgl. oben 12). Die durch den „Schiefstand“ des Topmastes angezeigte, weit ausgreifende Linienführung weist auf eine Flucht vom Ansatz des Topmastes in Höhe der Rahe bis zu einem mosaizistisch kunstvoll gearbeiteten pyramidalem Spitzdach auf quadratischem Grundriss. Dieses mit einem Pinienzapfen bekrönte Spitzdach, als Tempeldach gedeutet, zeigt wohl die genaue Route in die sich nach Südwesten öffnende, enge Hafeneinfahrt an: der Kurs ist dann richtig angelegt, wenn der Steuermann das Schiff so ausrichtet, dass Mast, Bug, die Seite einer Konstruktion mit Tonnengewölben steuerbord und das Spitzdach Bug voraus eine Flucht bilden.
14. Versetze die Strecke GM parallel zu AOB durch den Schnittpunkt 11 = Unterkante Segel.
15. Setze den Zirkel mit r = GE ein in O und schneide AOB heckwärts. Verbinde diesen Schnittpunkt mit Schnittpunkt 11. Verlängere diese Linie nach unten durch den Schiffsrumpf: die im Original (vgl. Abb.2) noch erkennbare Beschädigung der Bordwand steuerbord wird mittig geschnitten. Verlängere die Linie nach oben: auf ihr werden die Konstruktionspunkte EB1 – EB3 des Segels markiert. Die Linie begrenzt im Schnittpunkt 11 die Unterkante des Segels bugwärts.
16. Setze den Zirkel mit r = ME ein in M und schneide 14 = RS4. Begrenzung Unterkante des Segels heckwärts.
17. Ziehe den Zirkelschlag 16 weiter nach rechts und schneide die Linie 15 = EB3. Dieser Zirkelschlag ist mit äußerster Präzision auf der Segelfläche markiert.
18. Setze den Zirkel mit r = BE ein in D. Im Schnittpunkt mit der Senkrechten über M markiert das Kreisbogensegment die Daumenspitze der linken Hand des Matrosen. Ziehe den Kreisbogen weiter nach unten.
19. Setze den Zirkel mit r = BE ein in O und schneide den Kreisbogen 18 nach unten. Im Mosaik wird der Schnittpunkt durch den Aufsatz des 1. Wellensymbols ab Bug markiert.
20. In diesen Schnittpunkt 19 setze den Zirkel ein mit r = CE. Das Kreisbogensegment dieses Zirkelschlages ist erneut in der Segelfläche erkennbar mit äußerster Präzision verlegt und gibt die Höhe von RS3, im Schnittpunkt mit Linie 15 EB2 an.
21. In den Schnittpunkt 11 setze den Zirkel ein mit r = BE und schneide den Kreisbogen 20 = RS3.
22. Setze den Zirkel mit r = OA ein in G und schneide Kreisbogen 7 = RS2.
23. Setze den Zirkel mit r = ME ein in RS4 und schneide Linie 15 nach oben = EB1.
24. Setze den Zirkel mit r = OD ein in den Schnittpunkt 11 und markiere ein Kreisbogensegment heckwärts nach oben.
25. Setze den Zirkel mit r = OD ein in RS4 und schneide Kreisbogen 24 = RS1.
26. Setze den Zirkel mit r = OD ein in RS1 und schlage einen Kreisbogen bugwärts.
27. Setze den Zirkel mit r = CE ein in O und schneide Kreisbogen 26 = Begrenzung der Rahe bugwärts.
28. Verschiebe die Unterkante des Segels 14 parallel zu AOB nach oben durch RS1. Bis zum Schnittpunkt mit der Senkrechten über M = Rahe steuerbord.
29. In den Schnittpunkt 11 setze den Zirkel ein mit r = OE und schneide die Senkrechte über M nach oben = oberster Ansatz des Tauwerks.
30. Setze einen Entfernungsmesser ein in RS4 und rolle den Rand des Segels steingenau ab = OE.
31. Setze einen Entfernungsmesser ein in den Schnittpunkt 11 und rolle den Rand des Segels steingenau ab = OE.
32. Setze den Zirkel mit r = OS ein in 10 (Mastansatz heckwärts auf AOB). Der Kreisbogen heckwärts positioniert die Fingerspitzen der linken Hand des Segelführers und das Tau in seiner Hand bis zum Schnittpunkt mit der heckwärts verlängerten Linie 14 (Unterkante Segel und Ansatz Tau 2 am Segel).
33. Setze den Zirkel mit r = DE ein in die Spitze der Rahe bugwärts 27 und schneide den Kreisbogen 32 nach unten: Ansatz von Tau 1 (Zählung von oben nach unten) und Fingerspitzen der linken Hand. Insbesondere Mast und Segel belegen die Ableitung von Maßen aus dem gleichseitigen Fünfeck. Das sind alle Maße auf S oder E. (Dagegen können die Maße z.B. OA, OD, OC auch aus der Konstruktion eines Kreises abgeleitet werden). Schlagender Beweis sind die sorgfältigen Abbildungen der Radien ME und CE (=S5) auf der Segelfläche.
0.2.3.2.3. Die Rekonstruktion des Segels
Die vorgelegte Rekonstruktion des Segels ist das Ergebnis eingehender Betrachtung des Mosaikbildes. Es wird angenommen, dass die ganz exakt gelegten Kreisbogensegmente r = CE (s. Nr. 20) und r = ME (s. Nr. 17) auf der Segelfläche Hinweise auf eine präzise durchdachte Konstruktion sind, die „hinter“ dem Mosaik zu erkennen ist. Es wird weiter angenommen, dass das Segel durch einen Windwirbel bedingt im Mosaik in sich verdreht dargestellt ist. Die Spitzen, vier auf der linken und drei auf der rechten Seite des Segels, gehören nach dieser Annahme je zu einer Latte, deren Spitze zum Betrachter hin herausragt, während das andere Ende nach hinten gedrückt ist. Das Segeltuch wäre demnach mit fünf Latten quer versteift. Zusammen mit der Rahe und mit der über eine Latte fixierten Segelunterkante (im Gegensatz zum Hilfssegel des Seeruderschiffes, das nur an einer Rahe aufgehängt ist) sind es sieben Latten. Messtechnisch eindeutig nachweisbar ist das Verhältnis von Breite (= Länge der Rahe) zur Höhe des Segeltuches (= OE) wie 1:1,3 angegeben.
Das Mosaik bildet ab, wie ein Windwirbel das Segel nach steuerbord achtern herumreißt und dabei in sich verdreht. Dadurch liegt kein Druck mehr auf dem Steuerruder an, das Schiff ist manövrierunfähig und kränkt nach Steuerbord über. Die unmittelbare Gefahr des Kenterns besteht. Die Besatzung kann sich bei dieser Schlagseite nur noch auf den Knien aufrecht halten. Der Segelführer drückt sein rechtes Knie fest gegen die Bordwand steuerbord und stützt sich so ab. Ein Matrose klammert sich verzweifelt (Darstellung des weit aufgerissenen Auges, der Windwirbel zerzaust die Haare und lässt sie „zu Berge“ stehen) am gefährlich aus der Flucht gebogenen Mastbaum (Nr. 12) fest. Der Segelführer versucht entschlossen (Darstellung der viereckig gelegten Augen) unter Aufbietung aller Kräfte (Darstellung des vor Kraft strotzenden rechten Oberarmes, im Gegensatz dazu der „erlahmte“ Arm des Matrosen) und seines Körpergewichtes das Segel wieder unter Kontrolle zu bringen. Ist das abgebildete Herumschlagen des Segels, offensichtlich ermöglicht durch das Fehlen von Wanten und Stage (quer- und längsverspanntes Tauwerk zur Stabilisierung des Mastes), vielleicht auch ein Hinweis auf segeltechnische Möglichkeiten, die die Manövrierfähigkeit des Bootes in engen Segelrevieren verbessern könnte?

- Abb. 5: Der Aufriss des römischen Dschunken Segels mit Graphit auf Papyrus. (Rekonstruktionsversuch). Im Kompromiss zum Textbezug werden arabische Ziffern verwendet. Gesichert sind das Verhältnis von Breite zur Höhe, eine Mehrzahl von Latten, die in etwa symmetrisch ins Segeltuch quer eingezogen sind und die Verstärkung des Unterlieks (Unterseite des Rechtecksegels) durch eine Latte. Zur Diskussion gestellt werden die Anzahl, Breite und durch Mosaiksteine angegebenen Abstände der Querlatten. [Bild: Walther Krumme]
0.2.4.2.4. Die Konstruktion der Rumpfschale
34. In den Schnittpunkt 33 setze den Zirkel ein mit r = OD. Der Zirkelschlag von unten rechts ab G nach links oben bis zum Schnittpunkt mit Kreisbogen r = OA markiert die steil aufragende Bordwand backbord.
35. Setze den Zirkel mit r = CE ein in M und setze eine Markierung nach oben, die über RS1 liegt.
36. Setze den Zirkel mit r = CE ein in G und schneide Markierung 35.
37. In diesen Schnittpunkt 36 setze den Zirkel ein mit r = CE. Der Kreisbogen markiert die Bordwand backbord von G bis Höhe O und den Streifen auf dem linken Oberarm des Matrosen.
38. Der Kreisbogen r = DE, mit dem die Bordwand steuerbord konstruiert wird, wird angezeigt durch vier Wellen im Mosaik zwischen dem Kopf des Segelführers und dem steil aufragenden Hecksteven. Diese Wellen sind augenfällig auf einen Kreisbogen gelegt: Setze den Zirkel mit r = DE ein in E und schneide die Senkrechte über O. Setze den Zirkel mit gleichem r um in diesen Schnittpunkt. Von links unten nach links oben gezogen markiert dieser Kreisbogen die Lage der 4 Wellen, den Berührungspunkt des Gürtels des Segelführers mit der Bordwand backbord, den Punkt E, die Höhe der Bordwand steuerbord unter O.
39. Setze den Zirkel mit r = DE ein in RS2 und schneide BG, ziehe dann den Kreisbogen heckwärts bis zum Schnittpunkt mit r = OA um O = Bordwand steuerbord Heck.
40. Setze den Zirkel mit r = DE ein in RS2 und ziehe den Kreisbogen ab Schnittpunkt mit BG weiter bis zum Schnittpunkt mit der nach unten verlängerten Senkrechten über O = Bordwand steuerbord.
41. Halte den Zirkel mit r = DE im Schnittpunkt 40 und setze den Zirkelfuß um von RS2 auf die Senkrechte über O.
42. Ziehe den Kreisbogen r = DE jetzt weiter bis zum Schnittpunkt mit der nach unten verlängerten Senkrechten auf M, halte den Zirkel und setze den Zirkelfuß um auf den Schnittpunkt mit der ersten nach rechts konstruierten Sehne S5.
43. Ziehe den Kreisbogen r = DE weiter bis zum Schnittpunkt mit AOB.
44. Setze den Zirkel mit r = MB ein in M und schneide die Senkrechte über M nach oben.
45. In diesen Schnittpunkt 44 setze den Zirkel ein mit r = OS und schneide die Senkrechte über O nach unten, setze im Zirkelüberschlag den Fuß in diesen Schnittpunkt, schneide die nach unten durchgezogene Senkrechte durch M und ziehe den Kreisbogen bis etwa unter D = Kiel und Ansatz Bugsteven.
46. In den Schnittpunkt von Zirkelschlag 45 mit der nach unten verlängerten Senkrechten durch M setze den Zirkel ein mit r = CE und schlage einen Halbkreis nach oben. Der Kreisbogen bezeichnet von links nach rechts Mund und auch Fingerspitze 32 des Segelführers und begrenzt nach rechts zum Mosaikrand hin den „Kopf“ des „spindeldürren Wesens“ im Schneckenhaus.
47. In den Schnittpunkt von Zirkelschlag 45 mit der nach unten verlängerten Senkrechten durch M setze den Zirkel ein mit r = OA und ziehe einen Kreisbogen von links vom Schnittpunkt mit BE nach rechts bis unter den Bug: Auf dem Zirkelschlag lehnt der rechte Unterarm des Segelführers und der Halsansatz des „spindeldürren Wesens“ im Schneckenhaus. Das Schneckenhaus mit „Wesen“ steht also über ausgezogene Kreisbögen in Zusammenhang mit dem Segelboot, vgl. 77.
48. Setze den Zirkel mit r = OA ein in B und schneide Kreisbogen 47. In diesen Schnittpunkt setze den Zirkel ein mit r = OA und ziehe ein Kreisbogensegment vom Schnittpunkt 45 (unter M) bis zum Schnittpunkt mit der nach unten verlängerten Strecke CE = rekonstruierter Kiel, dann weiter durch B bis zur Höhe Unterkante Segel 14.
49. Zur Konstruktion des Heckstevens mit aufsitzender, schlichter Heckzier wird eine Konstruktionslinie benötigt: Setze den Zirkel mit r = AS ein in M und schneide die Senkrechte über M nach oben. Der Schnittpunkt wird auch durch die linke Daumenspitze des Matrosen angezeigt.
50. Setze den Zirkel mit r = OD ein in B und schlage einen Halbkreis nach oben von Schnittpunkt mit CE bis zur heckwärts verlängerten Strecke AOB. Der Zirkelschlag positioniert den Haaransatz des Segelführers und das Auge der aus dem Heck schießenden mythischen Schlange.
51. Durch den Schnittpunkt des Halbkreises mit r = OD 50 mit CE und durch den Schnittpunkt 49 ziehe eine Linie aus, die heckwärts Kreisbogen 50 schneidet.
52. Die Position des Schlangenkopfes und die Lage der Rumpfbemalung wird durch folgenden Zirkelschlag angegeben: setze den Zirkel mit r = CE ein in RS2 und ziehe von links oben nach rechts unten den Kreisbogen durch die heckwärts verlängerte Unterkante Segel 11 bis unter M. Dieser Kreisbogen begrenzt auch den Kopf der Schlange, bildet im Schnittpunkt mit Linie 51 den Konstruktionspunkt für den Hecksteven und ab Schnittpunkt mit AOB die Linienführung der Rumpfbemalung. (Der Zirkelschlag r = OD um diesen Konstruktionspunkt definiert die Position des Fisches an der Angel und teilt den Schwertfisch ab der zweiten Rückenflosse in eine abgebildete und eine konstruierte Hälfte).
53. Setze den Zirkel mit r = GE ein in B und ziehe ab Schnittpunkt mit heckwärts verlängerter Strecke AOB einen Halbkreis nach unten. Dieser Zirkelschlag formt die Schwanzflosse des Schwertfisches.
54. In den Schnittpunkt 53 setze den Zirkel ein mit r = OE und schneide Kreisbogen 52 nach oben: Konstruktionspunkt Abschluss Heckzier.
55. Setze den Zirkel mit r = DS ein in B und ziehe einen Halbkreis nach oben. Auf dem nach rechts gezogenen Bogen lehnt der Rücken des Segelführers.
56. Der steil aufragende Hecksteven wird mit „wandernden“ Zirkelschlägen r = OD konstruiert. Diese aneinandergesetzten Kreisbogensegmente sind im Mosaik deutlich zu erkennen, ein Hinweis, wie präzise es verlegt worden ist. Setze zunächst den Zirkel mit r = OD ein in B und schneide CE.
57. In diesen Schnittpunkt 56 setze den Zirkel mit r = OD um und ziehe einen Kreisbogen von B bis zum Schnittpunkt mit Linie 51 = Segment Hecksteven.
58. In diesen Schnittpunkt 57 setze den Zirkel um mit r = OD und schneide Kreisbogen 16.
59. In diesen Schnittpunkt 58 setze den Zirkel ein mit r = OD und verlängere den Hecksteven weiter nach oben bis zum Schnittpunkt mit Kreisbogen 55.
60. Setze jetzt in diesen Schnittpunkt 59 den Zirkel ein mit r = OD und ziehe eine Kreismarkierung in Verlängerung Heck.
61. Dann setze den Zirkel mit r = OD ein in den Schnittpunkt der Kreisbögen 48 und 50 und schneide Kreisbogen 60 nach unten.
62. Im Zirkelüberschlag wechsele den Standfuß des Zirkels mit r = OD auf Schnittpunkt 61 und ziehe dann ein Kreisbogensegment vom Schnittpunkt der Kreisbögen 48 und 50 nach unten bis zum Kreisbogen 55 = Segment Heckzier.
63. Die Ober- und Unterseite der Krümme Heckzier wird mit Zirkelüberschlägen r = AS konstruiert. Zunächst wird der Ansatz der Unterkante Krümme definiert: Setze den Zirkel mit r = OE ein in B und schneide Kreisbogen 52.
64. In diesen Schnittpunkt 63 setze den Zirkel ein mit r = AS und schlage einen Halbkreis nach unten.
65. Jetzt setze den Zirkel mit r = AS ein in den Schnittpunkt der Kreisbögen 50 mit 48 und schneide Halbkreis 64.
66. Im Zirkelüberschlag wechsele den Standfuß des Zirkels mit r = AS auf diesen Schnittpunkt 65 und ziehe ein Kreisbogensegment von 63 abwärts auf Kreisbogen 50 = Unterseite der Krümme.
67. Auch die steil aufragende Bordwand Heck backbord wird mit „wandernden“ Zirkelschlägen r = OD im Überschlag konstruiert. Der Zirkelschlag 34 ab G markierte den Ansatz der steil aufragenden Bordwand Heck backbord. In dessen Schnittpunkt mit der vierten Sehne S5 setze jetzt den Zirkel mit r = OD ein und schneide Kreisbogen 46.
68. In diesen Schnittpunkt 67 setze den Zirkel mit r = OD im Überschlag und ziehe den Kreisbogen ab S5 bis zum Schnittpunkt mit dem Kreisbogen 55 = Segment der steil aufragenden Bordwand Heck backbord.
69. In diesen Schnittpunkt 68 setze den Zirkel mit r = OD und schneide Kreisbogen 50 um B nach links.
70. In diesen Schnittpunkt 69 überschlage den Zirkel mit r = OD und ziehe einen Kreisbogen von Schnittpunkt 68 bis zum Schnittpunkt mit Kreisbogen 48.
71. Setze den Zirkel mit r = DE ein in RS3 und schneide den Kreisbogen 54, ziehe den Kreisbogen als Markierung weiter bis auf 50 nach unten= Abschluss der Heckzier
72. In den Schnittpunkt r = DE um RS3 71 mit Kreisbogen 54 setze den Zirkel mit r = AS und schneide Kreisbogen 52 nach unten.
73. Im Zirkelüberschlag halte den Zirkel mit gleichem r im Schnittpunkt 72 und schlage einen Halbkreis nach oben = Teilstück Schlangenrücken, Oberseite Krümme Heckzier bis Schnittpunkt mit Küstendarstellung.
0.2.5.2.5. Die Konstruktion des Bugschnabels
74. Setze den Zirkel mit r = GE ein in A und schneide den Kreisbogen r = OA um O nach oben = Bugspitze backbord. Versetze die 2. Sehne S5 parallel durch diesen Schnittpunkt = Buglippe. Ziehe diese parallel versetzte S5 wie einen Peilstrahl auf einer Seekarte weiter nach oben aus = Schnittpunkt mit der Einfahrt eines kleinen Hafens.
75. Setze den Zirkel mit r = OE ein in den Schnittpunkt 74 und markiere ein Kreisbogensegment nach unten.
76. Setze den Zirkel mit r = OE ein in D und schneide die Markierung 75.
77. In diesen Schnittpunkt 76 setze den Zirkel mit r = OE ein und ziehe ein Kreisbogensegment von D bis zum Schnittpunkt 74 = Bugschnabel backbord. Weiter nach rechts gezogen, trifft der Zirkelschlag das „Auge“ des „spindeldürren Wesens“ im Schneckenhaus vor dem Bug (vgl. 47).
78. Setze den Zirkel mit r = OD ein in A und markiere ein Kreisbogensegment nach unten.
79. Setze den Zirkel mit r = OA ein in M und schneide die Markierung 78.
80. Bugschnabel Unterseite, Bugsteven und Kiel werden mit drei Zirkelschlägen konstruiert. Dabei sind ausnahmsweise minimale Messtoleranzen beim Einsatz des Zirkels in M zu beachten. 1. In den Schnittpunkt 79 setze den Zirkel ein mit r = OD und ziehe ab A einen Kreisbogen nach links bis etwa unter D. 2. Daran anschließend setze den Zirkel mit r = OD ein in M und ziehe den Kreisbogen weiter heckwärts bis etwa zur durch M nach unten verlängerten Senkrechten. 3. Daran anschließend Kreisbogen 45.
81. Setze den Zirkel mit r = DS ein in A, schneide AOB und ziehe den Kreisbogen nach unten bis etwa unter S.
82. Setze den Zirkel mit r = DS ein in den Schnittpunkt 81 mit AOB und schneide den Kreisbogen nach unten.
83. In diesen Schnittpunkt setze den Zirkel mit r = DS und ziehe ein Kreisbogensegment von A bis zum Schnittpunkt mit AOB = Bordwand steuerbord Bugschnabel.
Damit ist nachgewiesen, dass der Bugschnabel mit insgesamt fünf Maßen des Victorinus-Codes zirkelkonstruiert worden ist. Jetzt kann im systemimmanenten Analogieschluss eine These zur Rekonstruktion des ausgebrochenen Buges des Seeruderschiffes aufgestellt werden: So wie der Bug des Segelbootes mit Maßen, generiert durch sein Pentagon, konstruiert wurde, so könnte auch der Bug des Seeruderschiffes mit Maßen seines Victorinus-Codes zirkelkonstruiert gewesen sein.
0.3.3. Vergleich der Konstruktion von Künstlersignatur und Segelboot
Es wird beobachtet, dass
1. die Künstlersignatur und das Segelboot nach dem gleichen Gestaltungsprinzip konstruiert sind: Alle Radien und Streckenmaße der Konstruktionszeichnung sowohl der Künstlersignatur als auch des Segelbootes lassen sich eindeutig aus der gezirkelten Konstruktion des Pentagons nach Ptolemäus ableiten,
2. der Punkt O des Durchmessers AOB sowohl in der Künstlersignatur als auch im Segelboot mosaizistisch besonders herausgehoben wird,
3. sowohl die Konstruktion des Pentagons der Künstlersignatur als auch die des Segelbootes durch die Süd-Nord Hauptachse des Mosaiks [Anm. 2] bestimmt wird: Der konstitutive Zirkelschlag (s. Nr.7), der die Sehne S5 definiert, wird stets in Richtung dieser Hauptachse ausgeführt,
4. ein Raster von Linien, parallel verschoben zur Strecke AOB, die Konstruktionen strukturiert,
5. Wellen gestrichelte Konstruktionslinien sichtbar machen,
6. Umrisse der Rümpfe von Fischernachen und Segelboot mit Kreisbögen des Victorinus-Codes konstruiert sind,
7. ausgezogene Konstruktionslinien sowohl der Künstlersignatur als auch des Segelbootes deren maritime und terrestrische Umgebung mitgestalten, z.B.: die Schwanzflosse des Schwertfisches achtern ist über r = GE um B konstruiert. (Ein Hinweis, dass die Zeichnung des Fisches wohl nicht von einer Vorlage kopiert sein kann, sondern zumindest innerhalb der Kreisfläche r = OD um den Konstruktionspunkt des Heckstevens 52 selbstständige Schöpfung ist. Ergänzend dazu auch die Beobachtung, dass der o.g. Kreisbogen den Fisch ab der zweiten Rückenflosse offenbar in konstruierte [alle Fischteile innerhalb dieser Kreisfläche] und phänomenologisch abgebildete Körperteile [alle Fischteile außerhalb der Kreisfläche] zerschneidet. Die heutigen Methoden zur Bestimmung einer Fischart können demnach nur auf den Fischkörper außerhalb der o.g. Kreisfläche angewendet werden). Das überdimensionale Schneckenhaus Bug voraus und die Schwanzflosse des Schwertfisches lehnt an r = OA um O und selbst die Position des Fisches an der Angel ist geometrisch „determiniert“ mit r = OD um den Konstruktionspunkt des Heckstevens 52, das Endstück der Angelschnur mit Haken = Kreisbogensegment mit o.g. Radius; dies alles bezeugt wieder, dass das Mosaik steingenau durchdacht und verlegt worden ist,
8. in der Künstlersignatur der nach unten durchgezogene Schwellzug des Buchstabens V(ICTORINUS) den Anstellwinkel des Heckspiegels definiert; beim Segelboot ein Peilstrahl über die Buglippe nach oben gezogen auf die Einfahrt eines kleinen Hafens (aus der Vogelperspektive) zielt,
9. ein einzelner Mosaikstein sowohl in der Künstlersignatur als auch im Segelschiff (Nr. 1) Träger mehrerer Informationen sein kann.
Die Annahme, dass die Künstlersignatur alle Gestaltungsprinzipien abbildet, die im Mosaik Verwendung finden [Anm. 6], wird bestätigt. Die Künstlersignatur ist der Schlüssel zum konstruktionsanalytischen Verständnis des Mosaiks. Das Konstruktionsprinzip des Victorinus-Codes im Oceanus-Mosaik Bad Kreuznach kann damit als bewiesen und der erkenntnistheoretische Ansatz opus tesselatum sui ipsius interpres (das Mosaik erklärt sich selbst) [Anm. 7] als bestätigt gelten.
0.4.4. Ausblick Analyse Segelboot
Mit der konstruktionsanalytischen Methode kann weiter nachgewiesen werden, dass sowohl die heutige, nach Wiedereinbettung in die Römerhalle verkantete Stellung der Mosaikschollen von Segelboot und seiner maritimen Umgebung unter der überbreiten Reparaturnaht unter dem Kiel, als auch die konservatorische Bearbeitung des Schiffrumpfes die ursprüngliche Dramatik, die der Schlüssel zum Verständnis des gesamten Mosaiks sein könnte, nicht mehr erkennen lässt: Ein extremes Manöver mit einem außergewöhnlichen Segel auf Leben und Tod auf schwer beschädigtem Schiff bei grenzwertiger Belastung von Mensch und Material.
0.5.5. Sind die Konstruktionszeichnungen für Schiff und Segel Dokumente römischer Schiffbautechnik?
Die Untersuchung „Der Victorinus-Code“ zeigte, dass sich aus dem geometrisch konstruierten Grundriss des Mosaiks der Architektenriss der Peristyl-Villa entfaltet.[Anm. 8] Die Angaben zur Lage der unterirdischen Stützmauer unter dem Garten der Villa sind im Mosaik geometrisch konstruiert enthalten und bautechnisch auch so zur Römerzeit umgesetzt worden. Ist durch diesen Befund der Analogieschluss zulässig: So wie die dechiffrierten geometrischen Konstruktionszeichnungen die Grundrisse von Mosaik und Villa in der Realität bautechnisch zutreffend wiedergeben, so werden auch mit dem Seitenriss des Segelbootes und dem Aufriss des Segels Konstruktionszeichnungen überliefert, die 1:1 in einer römischen Werft Anwendung fanden?
Weitere Fragen tun sich auf: Sind die Amphoren real abgebildet oder abbildungsähnlich konstruiert? Die Höhe der Amphoren ist über das Maß AS konstruiert. Es wird angenommen, dass hier die Methodik des kunstwissenschaftlichen Analogieschlusses genauso wenig greift wie die Methodik der vergleichenden Tierkunde beim Schwertfisch achtern. Hatte das Segelboot tatsächlich nur vier Amphoren geladen oder stehen die Amphoren vielleicht symbolisch für die Verteilung der Frachtlast: ¼ der Fracht direkt bugwärts vor den Mast, ¾ im Laderaum zwischen den Konstruktionspunkten O und G? Die konstruktionsanalytische Methodik unter der erkenntnistheoretischen Prämisse opus tesselatum sui ipsius interpres (das Mosaik erklärt sich selbst) ist zielführend bei der Rekonstruktion des ausgebrochenen Buges des Seeruderschiffes. Bei diesen Fragen stößt sie jedoch an Grenzen und ist der Ergänzung durch andere Methoden, z.B. der experimentellen Archäologie, bedürftig. Das Segelboot müsste nach den erschlossenen Konstruktionsangaben nachgebaut und mit dem Dschunken-Segel besegelt, auf Seetüchtigkeit, Wendigkeit und Belastbarkeit getestet werden, um sich der Beantwortung der o.g. Frage anzunähern.
0.6.6. Analyse der Bildinsel über dem Segelboot
Im folgenden Abschnitt wird versucht, u.a. mit konstruktionsanalytischen Experimenten die Bildinsel zu analysieren, die sich im Mosaik über dem Segelboot befindet. Schon unter Nr. 13 der Konstruktionsanalyse wurde beobachtet, dass der Topmast des Segelbootes den „demonstrativ provozierenden Schiefstand“ anzeigt, mit dem der römische Mosaizist Victorinus weit ausgreifende Linienführungen und Zusammenhänge im Mosaik verdeutlicht. In diesem Falle wird eine Verbindung von Segelboot und Bildinsel hergestellt und vermutet, dass eine ideale Route zur Hafeneinfahrt angezeigt worden ist. Es wird weiter beobachtet, dass die Mastspitze des Seeruderbootes auf der linken Seite des Mosaiks auf die Einfahrt eines natürlichen Hafens zielt, auf dessen in das Meer vorgeschobenen Kai Amphoren unter freiem Himmel umzäunt gelagert werden. Ein Berggipfel stellt die natürliche Spitze dieser Bildinsel dar.
Hypothetisch wird jetzt behauptet, dass Victorinus mit der Bildinsel über dem Segelboot den Typ des künstlich angelegten römischen Hafens mit geometrisch geformtem Hafenbecken und Gebäuden am Kai, im Gegensatz zum Typ Naturhafen links, darstellt.
Um der Argumentation prüfend folgend zu können, wird zunächst der Peilstrahl graphisch sichtbar gemacht (s. Abb. 6, grüner Pfeil), der aus dem demonstrativen Schiefstand des Topmastes erschlossen worden ist. Beobachtet wird, dass dieser Peilstrahl Architekturelemente in aufsteigender Reihenfolge aneinanderreiht:
- Eine ins Meer gebaute Konstruktion aus wuchtigen Tonnengewölben liegt vor der vermuteten Hafeneinfahrt und wird deshalb als Mole gedeutet.
- Die graphische Gestaltung der sehr engen, sich nach Südwesten öffnenden Hafeneinfahrt mit über das Lineal gezogenen Linien steht im künstlichen Gegensatz zum natürlichen Meeresbusen in der linken Bildinsel.
- Auf gleicher Höhe oder dicht hinter der Hafeneinfahrt liegt ein repräsentatives Gebäude mit umlaufender Säulengalerie.
- Der Peilstrahl visiert auf eine mit Lisenen verstärkte Wandfläche eines Gebäudes, das seine Entsprechung, jetzt ausnahmsweise im externen Analogieschluss, in der originalen Außenwand der Konstantin-Basilika zu Trier hat und möglicherweise ein kolossales Speichergebäude am Kai abbildet.
- Endpunkt des Peilstrahls ist der höchste Punkt der Bildinsel, ein pyramidales Spitzdach, bekrönt mit einem Pinienzapfen, und damit wohl als Tempeldach zu deuten. Hinter dem Ziegeldach des o.g. kolossalen Speichers liegend, ragt es ist räumlich heraus. Soll hier die Einfahrt in eine Hafenanlage angezeigt werden, in der das Segelboot operierte? Die Frage, ob dieser hypothetisch vermutete Hafen einem real existiert habenden römischen Hafen zugeordnet werden könnte, oder der vermutete Hafen aus Elementen verschiedener realer Häfen zusammen komponiert wurde, sprengt Methodik und Rahmen dieser Untersuchung.
Um den Nachweis zu führen, dass es sich bei der o.g. Bildinsel um den „Typ“ des römischen Kunsthafens handelt, wird versuchsweise nach einem Zusammenhang von Gebäudekulissen der Bildinsel und einem Hexagon gefragt.
In einem ersten konstruktionsanalytischen Experiment wird angenommen, dass
- das mit Wasser gefüllte Brunnenbecken (Herr Landesarchäologe Dr. Gerd Rupprecht hat den Wasser Zu- und Ablauf nachgewiesen) des Mosaiks den Auftraggeber wie ein Modell an ein künstlich angelegtes, hexagonales Hafenbecken erinnerte,
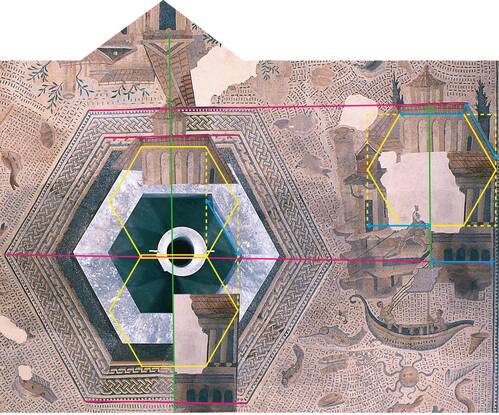
- die Gebäudekulisse des anzunehmenden Hafens über Konstruktionslinien des Hexagons seitlich nach rechts „verschoben“ worden sind (s. Abb. 6). Begründet wird diese Annahme durch den graphisch sichtbar gemachten Zusammenhang von Brunnenhexagon und Gebäudekulisse in Abb. 6: Die Höhe eines Ziegeldaches und damit die Lage des Tempeldaches wird durch die ausgezogene Sehne S6 begrenzt, die Tonnengewölbe fußen auf der ausgezogenen Mittelachse des Hexagons:
Können weitere Bezüge der „verschobenen“ Gebäudekulisse zu einem Hexagon nachgewiesen werden?
Dazu wird experimentell der hexagonale Grundriss des Brunnens (Innenmaß, gelb) mit dem Maß seiner Sehne S6 (blauer Pfeil) auf die Bildinsel gelegt:
Das Ergebnis des Experimentes ist evident:
1. Die gesamte Bildinsel ist ersichtlich über die geometrische Figur des Hexagons konstruiert.
2. Die Abbildungen der Gebäude sind sowohl in den Winkelmaßen 60° und 120° als auch in wiederkehrenden Abmessungen (blaue Pfeile) aus dem Innenmaß des Brunnenhexagons abgeleitet – wie Gebäude, die am Kai eines hexagonal angelegten Hafenbeckens angeordnet sind.
In einem 2. konstruktionsanalytischen Experiment werden die Gebäudekulissen der Bildinsel zunächst graphisch auseinandergeschnitten. Danach werden sie experimentell „zurück“ geschoben und dem „Modellhafenbecken“ (= Brunnenhexagon) zugeordnet. (Abb. 7: Gelbe durchgezogene und gepunktete Linien im Brunnenhexagon).
Es wird mit Abb. 7 festgestellt, dass sich die ausgeschnittenen Gebäudekulissen messtechnisch nachvollziehbar einem hexagonalen „Modellhafenbecken (= Brunnenhexagon) zuordnen lassen.
Es wird zur Diskussion gestellt, ob
- mit den experimentell zurückgeschobenen Kulissen Fragmente einer realen Hafenansicht einer künstlichen römischen Hafenanlage um 200 n. Chr. (die Forschung datiert das Mosaik auf 234 n. Chr.) sichtbar gemacht werden können,
- mit den zusammengeschobenen Gebäudekulissen der Bildinsel, wie es Victorinus im Mosaik abgebildet hat, ein römisches Piktogramm mit Anweisung zur Navigation in die Hafeneinfahrt eines tatsächlich existiert habenden römischen Kunsthafens vorliegt.
In den bisher durchgeführten konstruktionsanalytischen Experimenten wurde die linke Seite der Bildinsel mit dem Fragment eines Anglers ausgeschnitten und zunächst noch nicht berücksichtigt. Das wird wie folgt begründet:
Der o.g. Peilstrahl (Abb. 6) ist in seiner 1. Bedeutungsebene die nach oben und unten verlängerte Spiegelachse eines Hexagons, in der 2. Deutungsebene wohl eine Standlinie zur Navigation, in der 3. Deutungsebene die künstlerisch konstruktive Mittelachse der Bildinsel. Über diese künstlerische Mittelachse werden verschiedene Themen einander gegenübergestellt, z. B.:
- Die Wiedergabe von Perspektiven: Dem Versuch räumlicher Darstellung links durch eine Art Zentralperspektive wird die rein flächige Abbildung rechts (Konstruktion mit Tonnengewölben, Gebäude mit Säulengalerie) gegenübergestellt.
- Die Wiedergabe von Schlagschatten und Schattierung wird diskutiert: auf der linken Seite der Schlagschatten des rechten Fußes des Anglers, im Gegensatz dazu die meisterhafte Schattierung des pyramidalen Spitzdaches, die es plastisch aus der Bildfläche hervortreten lässt.
- Die Abbildung von Küstenlinien wird gegenübergestellt: auf der linken Seite schroffe Natürlichkeit, auf der rechten Seite mit dem Lineal gezogene Künstlichkeit, pointiert in der Darstellung eines kleinen Kunsthafens aus der Vogelperspektive (s. Konstruktionsanalyse Nr. 74).
Deshalb wird angenommen, dass die linke Seite der Bildinsel ein „biografischer Einschub“ in das Piktogramm sein könnte, der zur Identifizierung des Hafens nichts austrägt.
Die konstruktionsanalytischen Experimente haben die Annahme wahrscheinlich gemacht, dass Victorinus die Kulissen von Hafengebäuden und einem Peilpunkt (Tempeldach) um ein hexagonales Hafenbecken wie ein Piktogramm zur Navigation in Stein gelegt hat.
Auch das Dschunken Segel spricht für die Annahme eines Hafens als Einsatzort des Segelbootes, entfaltet es doch besonders in engen Revieren wie einem stark frequentierten Hafenbecken seine Vorteile.
Sollte mit dem Dschunken Segel auch ein Technologietransfer aus Fernost dokumentiert worden sein?
Nachweise
Verfasser: Walther Krumme
Red. Bearb.: Lutz Luckhaupt
Anmerkung:
Victorinus-Code ist als Marke unter der Nummer 30 2019 223 002 beim Deutschen Patent- und Markenamt eingetragen.
Verwendete Literatur:
Die vorgelegte Arbeit ist keine auf Literatur basierte Erörterung, sondern Protokoll der Entdeckungen und Experimente, die sich der konsequent deduktiven Methodik verpflichtet wissen, ohne die bisher geleistete Forschungsarbeit zum Thema herabsetzen oder ignorieren zu wollen.
Erstellt am: 12.04.2019
Anmerkungen:
- Krumme, W.: Der Victorinus-Code. In: http://www.regionalgeschichte.net/bibliothek/texte/aufsaetze/Krumme-der-victorinus-code.htlm [18.09.2018]. Dort weitere Literaturangaben. Zurück
- Krumme, W.: Der Victorinus-Code. In: http://www.regionalgeschichte.net/bibliothek/texte/aufsaetze/Krumme-der-victorinus-code.htlm [18.09.2018]. Dort weitere Literaturangaben. Zurück
- Krumme, W.: Der Victorinus-Code. In: http://www.regionalgeschichte.net/bibliothek/texte/aufsaetze/Krumme-der-victorinus-code.htlm [18.09.2018]. Dort weitere Literaturangaben. Zurück
- Krumme, W.: Der Victorinus-Code. In: http://www.regionalgeschichte.net/bibliothek/texte/aufsaetze/Krumme-der-victorinus-code.htlm [18.09.2018]. Dort weitere Literaturangaben. Zurück
- Krumme, W.: Der Victorinus-Code. In: http://www.regionalgeschichte.net/bibliothek/texte/aufsaetze/Krumme-der-victorinus-code.htlm [18.09.2018]. Dort weitere Literaturangaben. Zurück
- Krumme, W.: Der Victorinus-Code. In: http://www.regionalgeschichte.net/bibliothek/texte/aufsaetze/Krumme-der-victorinus-code.htlm [18.09.2018]. Dort weitere Literaturangaben. Zurück
- Krumme, W.: Der Victorinus-Code. In: http://www.regionalgeschichte.net/bibliothek/texte/aufsaetze/Krumme-der-victorinus-code.htlm [18.09.2018]. Dort weitere Literaturangaben. Zurück
- Krumme, W.: Der Victorinus-Code. In: http://www.regionalgeschichte.net/bibliothek/texte/aufsaetze/Krumme-der-victorinus-code.htlm [18.09.2018]. Dort weitere Literaturangaben. Zurück